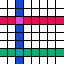

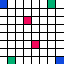

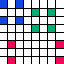
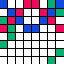

There are features that are pan within pan-magic square. They are patterns whose members add to a constant regardless of the position of the pattern within the pan-magic square, including positions that require wraparound. Among those features are the rows, columns, and diagonals of the square. These three are the minimum requirement for a pan-magic square. The complete and the {2compact2} features are the most commonly mentioned additional pan features. Dame Kathleen Ollerenshaw called pan-magic squares that also have both the complete and {2compact2} features most-perfect.
Within the order-8 pan-magic squares it is also possible to have the corners of all 3x3 and/or the corners of all 5x5 squares equal S/2. Since a {2compact2} (corners of 2x2 squares) square means that the corners of all 4x4 squares also equals S/2 (see proof) then all sub-square sizes within the order-8 square can be made equal to S/2. {Zigzag2} lines can also be pan within the magic square. {zigzag2} lines go back and forth between two rows or columns in the magic square, the 2 indicates that the {zigzag2} is between two adjacent lines. A {zigzag3} line would involve three adjacent lines. Zigzags will have an abababab pattern for the two lines, a and b, whereas Franklin W diagonals will have an abbaabba pattern.
There are other features that can be expressed within pan-magic squares that are not pan within the square. These features are only expressed in the magic square that is shown or in a limited number of other transformed squares. The associated property is the most commonly cited example of this type. Inlaid squares are also not pan within the larger pan-magic square but they are themselves pan-magic and may have different features than the larger square. Franklin bent diagonals are pan in one direction only. They are pan in the direction the V or W points but not laterally. Both V shaped and W shaped Franklin diagonals are possible in an order-8 square.
There are other patterns, both pan and non-pan within the magic square, that are present in some order-8 pan-magic squares. Some of these may be accidentally expressed in squares that are generated below but they are not directly supported.
There are 35 8-bit combinations of four zeros and four ones that start with zero. The order-8 A, B, and C base lines account for 11 of these. All combinations of these give valid base squares. There are eight additional lines (I call these asymmetric lines) from the set of 35 that make valid order-8 base squares when coupled with the A0 base line. There are undoubtedly other combinations of potential 16-bit, etc. base lines. These may introduce additional features but usually they are not considered here. In general, only the base figures that can be generated from the A, B, C, etc. type base lines are considered. The base squares with asymmetric base lines are included in the data set for the order-8 pan-magic square generator.
Added half rows feature to generator. This feature requires that each half of every row and every column add to S/2. It is one of the common features in Franklin squares. Not that feature is always true when order 4 squares are presnt in the quadrants. but it can be true on other cases as well.
monagonals  | {2compact2}  | associated  |
diagonals  | {2compact3}  | Franklin V  |
half rows  | {2compact5}  | Franklin W  |
complete  | {zigzag2}  | order-4 sq.  |
Added half rows feature to generator. This feature requires that each half of every row and every column add to S/2. It is one of the common features in Franklin squares. Note that feature is always true when order 8 squares are presnt in the quadrants, but it can be true on other cases as well.